Client Login
David Bain and the Balance of Probabilities
The purpose of Justice Binnie's investigation into the Bain case is to determine if David Bain is guilty "on the balance of probabilities." What does this mean? And is it possible for a judge to calculate actual probabilities?
Presumably the balance of probabilities means that the probability that David Bain is guilty exceeds the probability that he is not guilty. So some probabilities do have to be calculated.
But this isn't easy and definitely requires someone trained in the science and art of probability calculation. For examples of common errors there are the Prosecutor's Fallacy and the Defender's Fallacy. Then there's Simpson's Paradox and the False Positive Paradox and the Base Rate Fallacy. And of course the Kahneman and Tversky fallacies - the Conjunction Fallacy and the Availability Heuristic. All of these can occur in the examination of the evidence of the Bain case. Did Justice Binnie fall prey to these errors?
Further, the Bain evidence has the character that there is a lot of evidence that David is guilty but none of it is convincing on its own. How do you weigh up small amounts of evidence to come to an overall conclusion?. A juror could easily make the mistake of throwing out every single bit of evidence because it is not convincing on its own and conclude that the case is unproven when in fact the totality of the evidence is convincing. But how do you calculate the totality?
The probability calculations are too complicated for any human. We MUST use a computer. We illustrate how this can be done in this article.
We don't have access to the trial evidence or to Justice Binnie's report. So this article is only an illustration of how the calculation works. We offer no opinion or conclusion about the guilt or otherwise of David Bain. Let's start.
Which Probabilities?
We want to determine the probability that David is guilty given the evidence. We start with the probability that he is guilty without the evidence, put in the probabilities of the evidence given his guilt or otherwise, then use probability calculations to determine the updated probability of guilt with the evidence. Since he is presumed innocent we tend to bias all our probabilities in his favour when we make our assessments.
Whether David is guilty or not is a hypothesis which is a statement that we are unsure of and want to calculate the probability of. Hypotheses are illustrated with black-bordered boxes.
Evidence is a statement that we are sure of (some evidence may be controversial and doubtful and so it could become a hypothesis) and is illustrated with red-bordered boxes.
We know that either David or Robin committed the murders. In crimes of this nature it is usually the father who commits them. So without any evidence we start by assessing the probability that David is guilty as only 5%.
| P(David Guilty) | 0.05 |
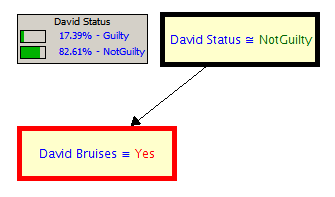
Now we introduce the evidence of the bruising and skin damage on David Bain. We need to calculate the probability of this damage given that he is guilty and also given that he is not guilty.
If he is not guilty then he is a normal active young man who gets a reasonable amount of skin damage. We asses this probability as 10%.
If he is guilty then he had a major fight to the death with his brother and so we asses the probability of damage as 40%. In summary
| Guilty | Not Guilty | |
|---|---|---|
| P(Bruises) | 0.4 | 0.1 |
Now given this evidence what is the probability that David is guilty? Our probability calculator tells us that it has jumped from 5% to 17.39%. The conclusion on the balance of probabilities is that David is not guilty. This is illustrated below in a network diagram.
More Evidence
Now we introduce the evidence of Robin's bruising and skin damage. There was none. The probabilities we assess are slightly tricky (be careful to remember that "Guilty" means that David is guilty, not Robin). Robin is older than David and less active so we assess that he only has a 5% chance of damage in normal life. But if he had a fight to the death with Stephen then he is very likely to have suffered damage so we put in a high probability of 60% of getting skin damage.
| Guilty | Not Guilty | |
|---|---|---|
| P(Bruises) | 0.05 | 0.6 |
Now the probability that David is guilty has risen to 33.33%.

Even More Evidence
Now we introduce the evidence of the note on the computer and the cartridge case balanced on its edge by Robin's body. It seems a bit strange to use a computer to write a suicide note. If David is guilty then we assess the probability that he would use a computer to write the note at 95%. If David is not guilty then Robin wrote the note but we think he would have likely used a pen and paper. So we assess the probability that he used the computer at 20%.
The cartridge case was balanced on its edge. If Robin shot himself we asses the probability of this at 1%. If David shot Robin and placed the cartridge case next to the body we asses the probability as 10%.
| Guilty | Not Guilty | |
|---|---|---|
| P(Used Computer) | 0.95 | 0.2 |
| P(Balanced) | 0.1 | 0.01 |
These two new pieces of evidence give a probability that David is guilty of 93.31%.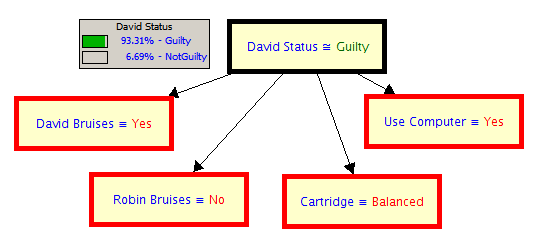
Another Hypothesis
Now to complicate things and to illustrate a new principle we introduce a new hypothesis. We hypothesise that Robin was depressed. It seems likely that he was depressed so we asses this probability as 60%.
| P(Robin Depressed) | 0.6 |
Now we have to modify the probability that David is guilty because if Robin is depressed then it is less likely that David is guilty. So if Robin is depressed we reduce our probability of David's guilt down from 5% to 1%. If Robin isn't depressed (i.e. normal) we keep this probability at 5% as before.
| Depressed | Normal | |
|---|---|---|
| P(David Guilty) | 0.01 | 0.05 |
We have to alter the probabilities of the note on the computer now because those probabilities depend on both hypotheses. Now it gets complicated. But that kind of proves our point that probability analysis can't be done mentally by humans.
We have to consider all combinations of the two hypotheses since the use of the computer depends on both. We assess the probabilities as:
David |
Guilty | Not Guilty | ||
|---|---|---|---|---|
| Robin | Depressed | Normal | Depressed | Normal |
| P(Used Computer) | 0.95 | 0.95 | 0.4 | 0.2 |
If David is guilty then Robin's state has no relevance so both probabilities stay at 95% as before. If Robin killed himself then would his depression affect the probability that he used the computer to write his suicide note? It might make him more likely to since the use of the computer seems to be a rushed note and indicative of a rushed mental state. So we put this probability at 0.4.
Now the probability of David's guilt has dropped to 88.21%.
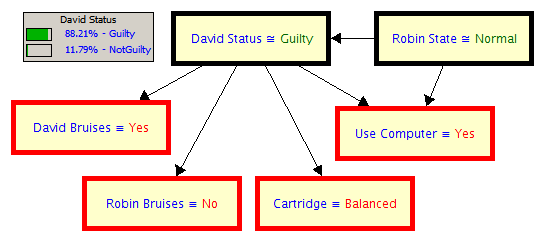
As a side benefit of this analysis we also get an update on the other hypothesis that Robin was depressed. Given the evidence the probability that he was depressed has dropped from 60% to 29.29%. The evidence of the note on the computer has reduced the likelihood that Robin committed suicide.
This analysis is an example of a Bayesian Network. It is obviously too simple at this stage and we aren't sure of the evidence anyway. To see how complicated such Bayesian networks can get enter the search term "Bayesian Network" into a Google image search.
Is David Bain guilty? We can't tell from this analysis but our feeling is that even though no one piece of evidence is convincing on its own the total mass of evidence will weigh up against him.
Contact us if you want any more information such as a copy of the .hugin file we used to create the network shown here. We would be interested in any networks you create too.